二項分布のポアソン近似
二項分布のポアソン近似![]() のもとで、
のもとで、![]() とすると二項分布はポアソン分布に収束する。
とすると二項分布はポアソン分布に収束する。
証明
積率母関数で証明する
現代数理統計学の基礎では積率母関数で証明する方法が紹介されています。この方法が一番単純なのでまず紹介します。
![]() が変数なので、
が変数なので、![]() とし変数を
とし変数を![]() だけにします。
だけにします。
![]()
![]() にして考えると、
にして考えると、![]() の定義から下のように収束します。
の定義から下のように収束します。
![]()
これはポアソン分布の積率母関数と一致するので、ポアソン分布に収束します。
確率関数で証明する
積率母関数で考える方法が一番簡単ではありますが、確率関数で考える方法もあります。データ解析のための数理統計入門ではこの方法が紹介されています。
二項分布の確率関数を下のように変形します。
![Rendered by QuickLaTeX.com \[p(k)=\frac{n!}{k!(n-k)!} (\frac{\lambda}{n})^k(1-\frac{\lambda}{n})^{n-k}=\frac{\lambda^k}{k!}(1-\frac{\lambda}{n})^n \frac{n!}{(n-k)!n^k}(1-\frac{\lambda}{n})^{-k}\]](https://busygamma.com/wp-content/ql-cache/quicklatex.com-cca179698703403c7fb0b0b9471c4c8a_l3.png)
![]() のとき、それぞれ4つがどうなるかというと、
のとき、それぞれ4つがどうなるかというと、
![]() は
は![]() が含まれていないので
が含まれていないので![]() はそのままになります。
はそのままになります。
![]() は
は![]() の定義からもわかる通り、
の定義からもわかる通り、![]() に収束します。
に収束します。
![]() は下のように変形できます。
は下のように変形できます。
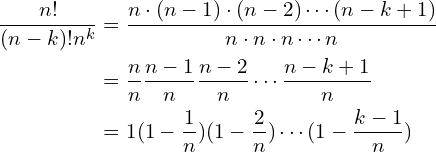
それぞれ![]() に収束するので、積も
に収束するので、積も![]() に収束する。
に収束する。
![]() は
は![]() は0に収束するので、1の
は0に収束するので、1の![]() 乗と考えることができるので、1です。
乗と考えることができるので、1です。
よって確率関数は
![Rendered by QuickLaTeX.com \[\lim_{n \to \infty} p(k) = \lim_{n \to \infty} \frac{\lambda^k}{k!}(1-\frac{\lambda}{n})^n \frac{n!}{(n-k)!n^k}(1-\frac{\lambda}{n})^{-k} = \frac{\lambda^k}{k!} e^{-\lambda}\]](https://busygamma.com/wp-content/ql-cache/quicklatex.com-ae762dd2e3f9e531232bc88f2b6930b0_l3.png)
このように収束し、この確率関数はポアソン分布と一致します。


