平均![]() 分散
分散![]() のランダムサンプルを考える。
のランダムサンプルを考える。
![]()
このときに標本分散![]() の期待値と分散を考える。標本分散の定義とは
の期待値と分散を考える。標本分散の定義とは![]() である。
である。![]() はサンプルサイズである。
はサンプルサイズである。
![]() をまず変形したい。シグマの中を
をまず変形したい。シグマの中を![]() を引いて
を引いて![]() を足してみる。
を足してみる。
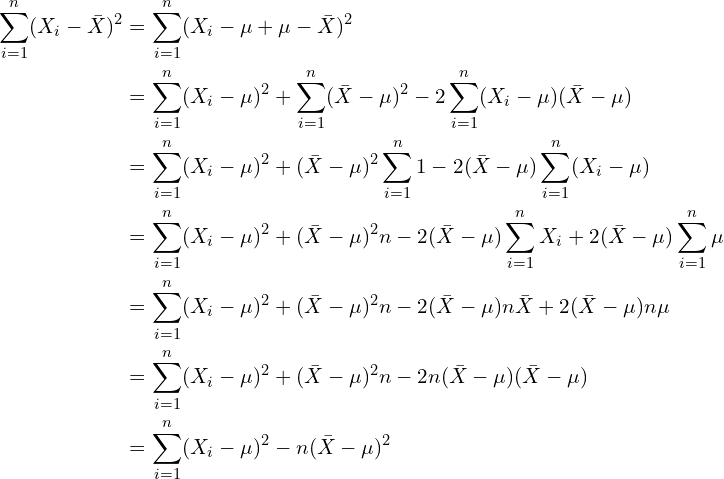
![]() と変形できる。
と変形できる。
![Rendered by QuickLaTeX.com $$\begin{align}E[\sum^n_{i=1} (X_i-\bar{X})^2]&=E[\sum^n_{i=1} (X_i-\mu )^2 - n(\bar{X}-\mu )^2] \\&= E[\sum^n_{i=1} (X_i-\mu )^2]-nE[(\bar{X}-\mu )^2] \\&= \sum^n_{i=1} E[ (X_i-\mu )^2]-nE[(\bar{X}-\mu )^2] \\&= \sum^n_{i=1} E[ (X_i-E[X_i] )^2]-nE[(\bar{X}-E[\bar{X}] )^2] \\&=n \sigma^2-n\frac{\sigma^2}{n} = \sigma^2(n-1)$\end{align}$$](https://busygamma.com/wp-content/ql-cache/quicklatex.com-8155359ab381bf047bb98b6ec5c6b2a6_l3.png)
![]() の期待値は
の期待値は![]() になる。
になる。![]() を不偏分散という。
を不偏分散という。
 数理統計
数理統計平均![]() 分散
分散![]() のランダムサンプルを考える。
のランダムサンプルを考える。
![]()
このときに標本分散![]() の期待値と分散を考える。標本分散の定義とは
の期待値と分散を考える。標本分散の定義とは![]() である。
である。![]() はサンプルサイズである。
はサンプルサイズである。
![]() をまず変形したい。シグマの中を
をまず変形したい。シグマの中を![]() を引いて
を引いて![]() を足してみる。
を足してみる。
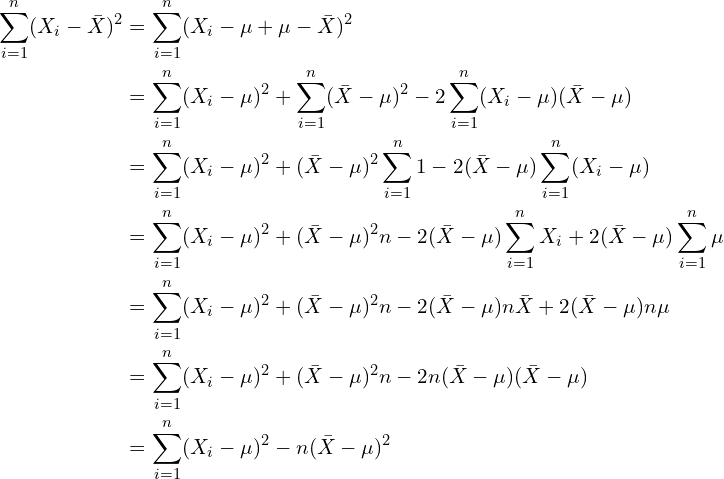
![]() と変形できる。
と変形できる。
![Rendered by QuickLaTeX.com $$\begin{align}E[\sum^n_{i=1} (X_i-\bar{X})^2]&=E[\sum^n_{i=1} (X_i-\mu )^2 - n(\bar{X}-\mu )^2] \\&= E[\sum^n_{i=1} (X_i-\mu )^2]-nE[(\bar{X}-\mu )^2] \\&= \sum^n_{i=1} E[ (X_i-\mu )^2]-nE[(\bar{X}-\mu )^2] \\&= \sum^n_{i=1} E[ (X_i-E[X_i] )^2]-nE[(\bar{X}-E[\bar{X}] )^2] \\&=n \sigma^2-n\frac{\sigma^2}{n} = \sigma^2(n-1)$\end{align}$$](https://busygamma.com/wp-content/ql-cache/quicklatex.com-8155359ab381bf047bb98b6ec5c6b2a6_l3.png)
![]() の期待値は
の期待値は![]() になる。
になる。![]() を不偏分散という。
を不偏分散という。